Yeah, well, there’s nothing rose in terms of accuracy. I’m waiting on people’s responses on the accuracy of War Room and Global War before thinking about purchasing them.
Supreme map for 1941
-
Hi Orillian,
Are you really sharing your map file? I thought we could only by the printed enlarged version.
If youre saying that we can have it, then I want it Otherwise, sorry for asking…
-
Hi Orillian
Who is Orillian?
Are you really sharing your map file
That’s the use of this thread.
I thought we could only by the printed enlarged version
What do you mean by “by” (buy?)? There’s nothing to buy, the files are for free.
-
Hi dedo
First can I say thanks for all your hard work on this. The result looks great.
I am intending to get the 1129x600mm version printed and note that BananeDC used “450gr anti-fire stuff”. Obviously I would ask the printer’s advice but wondered whether you had a recommendation?
Thanks again.
Cheers
PP -
Thank you for giving kudos to me!
I take so called Blockout Banner (760gr/qm) or PVC Banner (510gr/qm) with antiglare. Both can be printed with a solution of 720 dpi, inks should be a mild or eco solvent.
It is important to take heavy ware (a lot of gr/qm). This kind of quality lays perfectly on a table and could be furled easily by avoiding folds.
-
Thanks very much for the advice dedo.
Cheers
PP
-
Can anyone recommend or suggest a venue for printing this. I went into my local office max who has printing services and they looked at me like I have two heads…
-
My brother printed 3 maps for myself and friends in the UK. He has his own small print business, but actually sourced them from Italy.
Where are you?
-
Ah, alas, I am state side. New York area to be exact. Any other ideas?
-
Unfortunately, I can’t recommend a special shop because I’m from Germany but instead I recommend you to do an internet search with the following search terms:
canvas printing, vinyl banner printing, eco solvent printing, New York -
Thanks. I appreciate the advice, I will begin my hunt…
-
Just as a public service, I had the 1941 Supreme map (1329x700mm, or 52x28") printed at my local Fed-Ex Office print shop on outdoor banner vinyl. It cost me about $70 (US dollars) to have this done. I know not everyone will get the same prices or print the same size, but that’s just to give a ball park figure in 2016 dollars of what a typical big box print shop will charge for such a project. Kudos to Dedo for making this available to the A&A community! Two pics below include one shot ready to play, and another showing the size difference between the printed map and the original board map. Here’s my results:

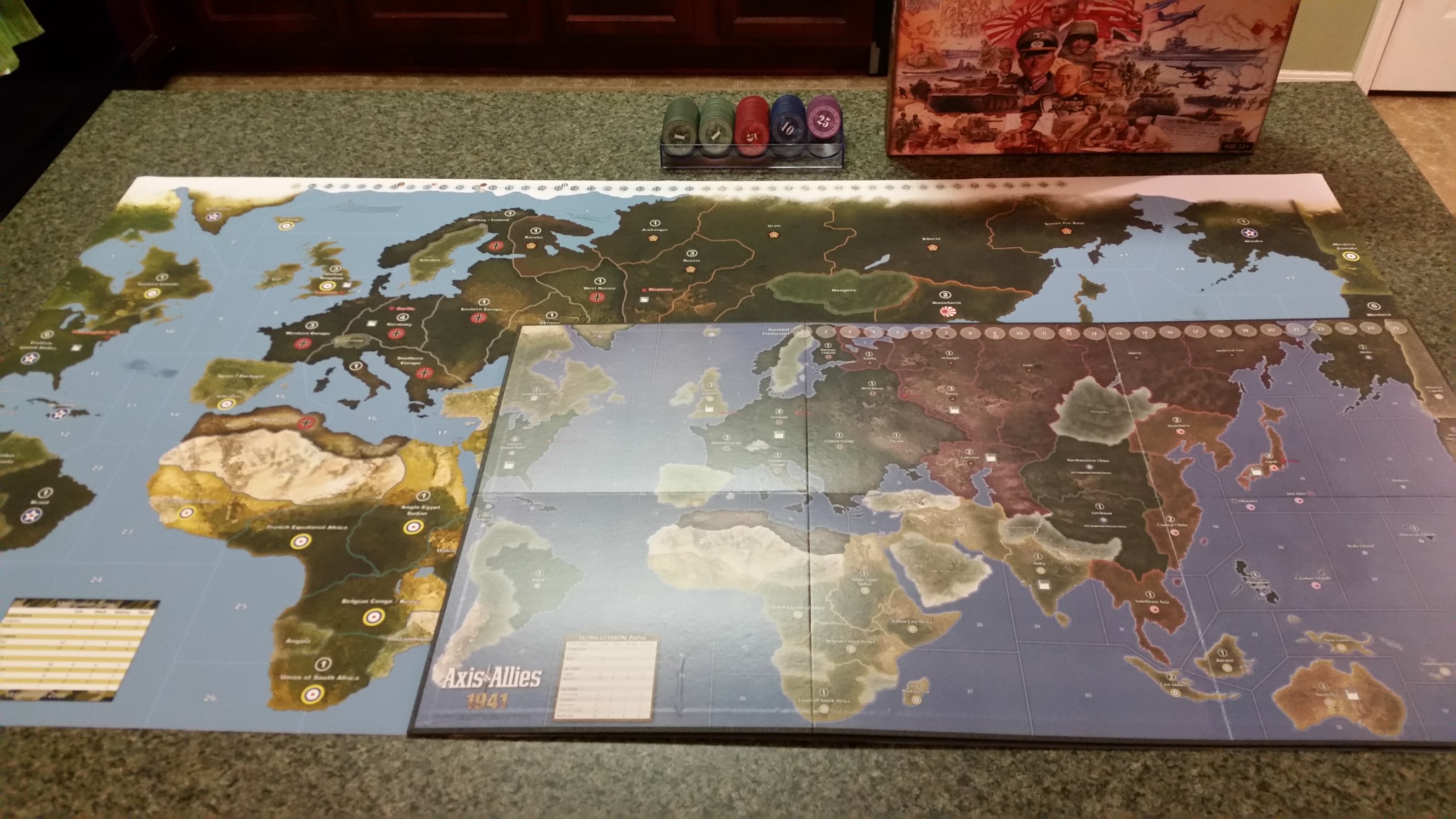
-
 P Panther locked this topic on
P Panther locked this topic on





